praboum.free.fr

$python_icon$

1) Identité et Théorème de Bézout
2) Lemmes d'Euclide et de Gauss
3) Petit Théorème de Fermat
4) Analyse
5) Probabilités
6) Algèbre
7) Valeurs à connaître

1) Identité et Théorème de Bézout

1.1) Théorème de Bachet-Bézout (ou Identité de Bézout)

Théorème: Soit $a$ et $b$ deux entiers relatifs et $d=PGCD(a,b)$, alors il existe deux entiers relatifs $u$ et $v$ tels que $au+bv=d$.

Par l'absurde, supposons qu'il existe deux entiers relatifs $u$ et $v$ tels que $au+bv=k$, où $k$ est un entier relatif non multiple de $d$.
Alors $d|a$ et $d|b$, donc $d|k$ ce qui contredit notre hypothèse. Autrement dit si $k$ est un nombre entier non multiple de $d$, alors il n'existe pas d'entiers $u$ et $v$ tels que $au+bv=k$.

1.2) Théorème de Bézout

Théorème: deux entiers relatifs $a$ et $b$ sont premiers entre eux ssi il existe deux entiers relatifs $u$ et $v$ tels que $au+bv=1$.

Démonstration par double implication:
$\Rightarrow$
Supposons que $a$ et $b$ sont premieurs entre eux, alors $PGCD(a,b)=1$ et d'après l'identité de Bézout, il existe $(u,v)$ tels que $au+bv=1$

$\Leftarrow$
Supposons qu'il existe $(u,v)$ d'entiers relatifs tels que $au+bv=1$, et soit $d=PGCD(a,b)$. Alors $d|a$ et $d|b$, donc $d|1$ et $d=1$ ce qui signifie que $a$ et $b$ sont premiers entre eux.

Démonstration par double implication:
$\Leftarrow$
Supposons qu'il existe $(u,v)$ d'entiers relatifs tels que $au+bv=1$, et soit $d=PGCD(a,b)$. Alors $d|a$ et $d|b$, donc $d|1$ et $d=1$ ce qui signifie que $a$ et $b$ sont premiers entre eux.

$\Rightarrow$
Supposons que $a$ et $b$ sont premiers entre eux, et considérons l'ensemble des entiers $\mathcal E$ relatifs de la forme $au+bv$ où $u$ et $v$ sont des entiers relatifs.
L'ensemble $\mathcal E \cap \mathbb{N}^* $ n'est pas vide, en effet:
- si $a > 0$, alors $a\times1+b\times0=a \in \mathcal E$
- si $a < 0$, alors $a\times(-1)+b\times0=-a \in \mathcal E$.
Il existe donc un plus petit élément $n_0 \in \mathcal E \cap \mathbb{N}^* $, tel que $au_0+bv_0=n_0$.
$a=n_{0}q+r$ avec $0 \leq r < n_0$, donc:
$r=a-q(au_0+bv_0)=a(1-qu_0)-bqv_0$, donc $r \in \mathcal E$.
On vient donc de montrer que $r \in \mathcal E$, mais $0 \leq r < n_0$, donc $r \notin \mathbb{N}^* $, et finalement $r=0$, ce qui signifie que $n_0|a$.
De la même manière on montre que $n_0|b$; or $a$ et $b$ sont premiers entre eux, donc $n_0=1$.
On a donc bien montré qu'il existe un couple $(u_0;v_0)$ tel que $au_0+bv_0=1$.

Exemple d'application: Résoudre une équation dans $\mathbb{Z}/n\mathbb{Z}$
Rappel, si $n=p$ est premier, alors tous les éléments non nuls de $\mathbb{Z}/p\mathbb{Z}$ sont inversibles (l'anneau $\mathbb{Z}/p\mathbb{Z}$ est alors un corps).
Sinon, soit $a$ un élément de $\mathbb{Z}/n\mathbb{Z}$, alors $a$ est inversible ssi $a$ est premier avec $n$.

$a$ est premier avec $n$
$\Leftrightarrow \exists (u,v) \in \mathbb{Z}^2, au+nv=1$.
$\Leftrightarrow \exists (u,v) \in \mathbb{Z}^2, au-1=-nv$.
$\Leftrightarrow \exists (u,v) \in \mathbb{Z}^2, au-1=0$ dans $\mathbb{Z}/n\mathbb{Z}$.
$\Leftrightarrow a$ est inversible.

Supposons qu'on doive résoudre dans $\mathbb{Z}/63\mathbb{Z}$, l'équation $37x=1$.
Il nous faut donc déterminer l'inverse de $37$ dans $\mathbb{Z}/63\mathbb{Z}$.
En appliquant l'algorithme d'Euclide, on trouve $10 \times 63 -17 \times 37 =1 $
Or dans $\mathbb{Z}/63\mathbb{Z}$, $63=0$ ce qui donne $-17\times 37=1$ donc -17=46 est l'inverse de $37$ et finalement $x=46$.

1.3) Théorème de la récursivité pour le PGCD

Soient deux entiers naturels $a$ et $b$, alors $PGCD(a,b)=PGCD(b,a-b)$. On constate donc qu'on peut réaliser autant de différence que l'on veut.
Théorème: Si on note la division euclidienne $a=bq+r$, alors on a $PGCD(a,b)=PGCD(b,r)$.

Démonstration par double inclusion:
Notons $\mathcal{D}_a$ l'ensemble des diviseurs de $a$, $\mathcal{D}_b$ l'ensemble des diviseurs de $b$ et $\mathcal{D}_r$ l'ensemble des diviseurs de $r$.
$\subset$
Soit $d \in \mathcal{D}_a \cap \mathcal{D}_b$.
Alors $d|a$ et $d|b$, donc $d$ divise n'importe quelle combinaisons linéaire de $a$ et $b$, donc $d$ divise $r=a-bq$, donc $d \in \mathcal{D}_b \cap \mathcal{D}_r$
$\supset$
Soit $d \in \mathcal{D}_b \cap \mathcal{D}_r$.
Alors $d|b$ et $d|r$, donc $d$ divise n'importe quelle combinaisons linéaire de $b$ et $r$, donc $d$ divise $a=bq+r$, donc $d \in \mathcal{D}_a \cap \mathcal{D}_b$
On a obtenu que $\mathcal{D}_a \cap \mathcal{D}_b=\mathcal{D}_b \cap \mathcal{D}_r$, et donc $PGCD(a,b)=PGCD(b,r)$

1.4) Algorithme d'Euclide

L'algorithme d'Euclide est basé sur le résultat précedent: $PGCD(a,b)=PGCD(b,r)$.
Pour calculer un $PGCD$, on effectue donc des divisions successives.
Mais comment déterminer les entiers relatifs $u$ et $v$? Toujous avec l'algorithme d'Euler.

Exemple:
Calculer $PGCD(170,65)$, puis déterminer $(u,v)$ tels que $170u+65v=PGCD(170,65)$.
170=65x2+40
65=40x1+25
40=25x1+15
25=15x1+10
15=10x1+5
10=5x2+0
On trouve donc $PGCD(170,65)=5$.
Méthode pour trouver les entiers relatifs $u$ et $v$, on remonte:
5=15-10=(40-25)-(25-15)=40-2x25+40-25=2x40-3x25
5=2x40-3x(65-40)=5x40-3x65=5x(170-2x65)-3x65=5x170-13x65
On a donc obtenu 5=5x170-13x65, soit $u=5$ et $v=-13$.
De plus $au+bv=a(u-b)+b(v+a)$, il y a donc une infinité d'entiers relatifs tels que $au+bv=PGCD(a,b)$.

Exemple (PGCD de 2 polynômes):
Calculer le PGCD dans $K[X]$($K$ étant $R$ ou $C$) des polynômes $A$ et $B$ suivants:
$A(X)=X^5-2X^4+X^3-X^2+2X-1$
$B(X)=X^3-X^2+2X-2$
On procède exactement de la même façon.
$X^5-2X^4+X^3-X^2+2X-1$$=(X^3-X^2+2X-2)(X^2-X-2)$$+X^2+4X-5$
$X^3-X^2+2X-2$$=(X^2+4X-5)(X-5)+27(X-1)$
$X^2+4X-5$$=(X-1)(X+5)+0$
Le p.g.c.d. de $A$ et $B$ aussi noté $A \wedge B$ est donc $X-1$.

Rappel: Pour calculer le PPCM, on pourra utiliser la formule $ab=PGCD(a,b) \times PPCM(a,b)$

2) Théorème de Gauss et lemme d'Euclide

Théorème: si $a$ divise $bc$ et si $a$ est premier avec $b$, alors $a$ divise $c$.

$a | bc$, donc $\exists k \in \mathbb{Z}, bc=ka$.
$a$ est premier avec $b$, donc d'après le théorème de Bézout, $\exists (u,v)\in \mathbb{Z}^2$ tel que $au+bv=1$, donc en multipliant cette dernière relation par $c$ on a:
$c=acu+bcv$.
Or $bc=ka$, donc $c=acu+kav=a(cu+kv)$ avec $cu+kv \in \mathbb{Z}$, donc $a|c$.

Lemme (d'Euclide): Soient $b$ et $c$ deux entiers. Si un nombre premier $p$ divise le produit $bc$, alors $p$ divise $b$ ou $c$.

Nous allons utiliser le théorème de Gauss.
Posons $d=PGCD(p,b)$, alors $d|p$ autrement dit comme $p$ est un nombre premier $d=1$ ou $d=p$.
Si $d=1$, alors $p$ et $b$ sont premiers entre eux et donc d'après le théorème de Gauss $p|c$.
Si $d=p$, alors $p=PGCD(p,b)$ et donc $p|b$.

3) Petit Théorème de Fermat

Théorème: soit $p$ un nombre premier et $a \in \mathbb{Z}$. Alors $a^p \equiv a [p]$. On dit que $a^p$ est congru à $a$ modulo $p$.
De plus, si $p$ est premier avec $a$, alors: $a^{p-1} \equiv 1 [p]$.

Lemme utilisé dans la démonstration:
Si $k \in \{1,2,\ldots, p-1\}$, alors $p| \binom{p}{k}$.
Preuve de ce lemme:
$\binom{p}{k}=\frac{p!}{k!(p-k)!}=\frac{p(p-1)!}{k(k-1)!((p-1)-(k-1))!}$, d'où $k\binom{p}{k}=p\binom{p-1}{k-1}$, donc $p|k\binom{p}{k}$.
Or $p$ est un nombre premier et $k < p$, donc $p$ et $k$ sont premiers entre eux, donc d'après le théorème de Gauss, $p|\binom{p}{k}$.

Montrons que pour tout $a \in \{1,2,\ldots, p-1\}$, on a $a^p \equiv a [p]$.
Par récurrence:
Initialisation: On a $0^p=0 \equiv 0 [p]$
Hérédité: Soit $a \in \{1,2,\ldots, p-2\}$,et supposons que $a^p \equiv a [p]$.
Alors $(a+1)^p=\displaystyle \sum_{k=0}^{p} \binom{p}{k} a^k$.
$ \Leftrightarrow (a+1)^p=a^p+ \displaystyle \sum_{k=1}^{p-1} \binom{p}{k} a^k +1$
Or d'après le lemme précédent, pour $k \in \{1,2,\ldots, p-1\}$, $\binom{p}{k} \equiv 0 [p]$, donc $\displaystyle \sum_{k=1}^{p-1} \binom{p}{k} a^k \equiv 0 [p]$ et donc:
$(a+1)^p \equiv a+0+1 [p]$
$(a+1)^p \equiv a+1 [p]$
Conclusion si la propriété est vraie au rang $a$, elle est encore vraie au rang $a+1$, ce qui démontre le petit théorème de Fermat.

4) Analyse

4.1) Suites numériques

Soit $ (u_n)_{n \in \mathbb{N}} $ une suite géométrique de raison $q \neq 1$. Alors, $S_{n}=\displaystyle \sum_{k=0}^{n} u_k=\displaystyle \sum_{k=0}^{n} u_{0}q^{k}=u_{0}\frac{1-q^{n+1}}{1-q}$

Soit $S=\displaystyle \sum_{k=0}^{n} q^{k}=1+q+q^{2}+...+q^{n-1}+q^{n}$, alors:
$S-qS=\displaystyle \sum_{k=0}^{n} q^{k}-q^{k+1}=1-q^{n+1}$,d'où:
$S_{n}=u_{0}\frac{1-q^{n+1}}{1-q}$

Soit $ (u_n)_{n \in \mathbb{N}} $ une suite arithmético-géométrique, c'est-à-dire que $\forall n \in \mathbb{N}$, $u_{n+1}=au_n+b$.
Alors, $u_n=a^n (u_0-r)+r$ où $r$ est le point fixe càd $r=\dfrac{b}{1-a}$.

Posons $v_n=u_n-r$, alors $v_{n+1}=u_{n+1}-r$
$ \Leftrightarrow v_{n+1}=au_n+b-r$
$ \Leftrightarrow v_{n+1}=a(v_n+r)+b-r=av_n$
$(v_n)$ est donc géométrique, et $v_n=v_0 a^n$, d'où $u_n=v_0 a^n +r=(u_0 -r)a^n +r$

4.2) Suites adjacentes

Définition: Deux suites réelles $(a_n)$ et $(b_n)$ sont dites adjacentes si l'une est croissante, l'autre décroissante et si la différence des deux converge vers 0.
Théorème (des suites adjacentes): Soient $(a_n)$ et $(b_n)$ deux suites adjacentes. Alors ces deux suites sont convergentes et ont la même limite $l \in \mathbb{R}$.
De plus, pour tout entier naturel $n$, $a_n ≤ l ≤ b_n$ (où $(a_n)$ est croissante et $(b_n)$ décroissante).

4.3) Suite récurrente

Soit $f$ est une fonction continue sur un intervalle $I$ à valeurs réelles.
On étude la suite $u_n$ définie par $u_0 \in I$ et pour tout $n \in \mathbb{N}$, $u_{n+1}=f(u_n)$.
Définition: On dit qu'un intervalle $J$ est stable par $f$ si $f(J) \subset J$

Propriété 1: Soit $f : I → \mathbb{R}$ et $J \subset I$ un intervalle stable par $f$. Si $u_0 \in J$, alors la suite $(u_n)_{n \in \mathbb{N}}$ est bien définie et $u_n \in J$ pour tout $n \in \mathbb{N}$.

Propriété 2 (monotonie de $u_n$):
Soient $f : I \rightarrow \mathbb{R}$ avec $I$ stable par $f$ et $(u_n)_{n \in \mathbb{N}}$ définie par $ \left\{ \begin{array}{ll} u_0 \in I \\ \forall n \in \mathbb{N}, u_{n+1}=f(u_n) \end{array} \right. $
Si $f$ est croissante sur $I$ alors la suite $(u_n)$ est monotone :
1. Si $u_1 ≥ u_0$, alors $(u_n)$ est croissante.
2. Si $u_1 ≤ u_0$, alors $(u_n)$ est décroissante.

Démonstration par récurrence.

Propriété 3:
Soient $f : I \rightarrow \mathbb{R}$ avec $I$ stable par $f$ et $(u_n)_{n \in \mathbb{N}}$ définie par $ \left\{ \begin{array}{ll} u_0 \in I \\ \forall n \in \mathbb{N}, u_{n+1}=f(u_n) \end{array} \right. $
Si $f$ est décroissante sur $I$, alors les suites extraites $(u_{2n})$ et $(u_{2n+1})$ sont monotones et de monotonie contraire.

Posons $g = f \circ f$. Cette application est croissante sur $I$. Posons $v_n = u_{2n}$ et $w_n = u_{2n+1}$.
Les deux suites vérifient $v_{n+1} = u_{2n+2} = f(u_{2n+1}) = f(f(u_{2n}))$ $= g(u_{2n}) = g(v_n)$ et de même $w_{n+1} = g(w_n)$.
La propriété 2 permet alors d’en déduire que chacune des suites $(v_n)$ et $(w_n)$ est monotone.
Supposons, par exemple que $(v_n)$ est croissante. On peut donc écrire, pour tout $n \in \mathbb{N}$ : $v_n ≤ v_{n+1}$.
En appliquant la fonction $f$ décroissante, on en déduit $f(v_n) ≥ f(v_{n+1})$ c’est-à-dire $w_n ≥ w_{n+1}$. La suite $(w_n)$ est donc décroissante.
Si l’on suppose désormais que la suite $(v_n)$ est décroissante, on peut déduire de la même manière que $(w_n)$ est croissante.

4.4) Suites et Séries de fonctions

Continuité: Soit $I$ un intervalle et $(f_n)$ une suite de fonctions continues de $I$ dans $\mathbb{R}$ qui converge uniformément vers $f$ sur $I$. Alors $f$ est continue.

Soit $u_n$ une suite de fonctions continues en $a \in I$. On suppose que $\sum_n u_n$ converge uniformément vers $S$ sur $I$. Alors $S$ est continue en $a$. En particulier, si toutes les $u_n$ sont continues sur $I$, alors $S$ est continue sur $I$.

Dérivabilité: Soit $I$ un intervalle, $(f_n)$ une suite de fonctions $\mathcal C^1$ de $I$ dans $\mathbb{R}$ et $f,g:I→\mathbb{R}$. On suppose que:
- $(f_n)$ converge simplement vers $f$ sur $I$.
- $(f'_n)$ converge uniformément vers $g$ sur $I$.
Alors la fonction $f$ est de classe $\mathcal C^1$ et $f'=g$.

Soit $u_n$ une suite de fonctions de classe $\mathcal C^1$ sur $I$. On suppose que:
- $\sum_n u_n$ converge simplement sur $I$.
- $\sum_n u'_n$ converge uniformément sur tout segment contenu dans $I$.
Alors la fonction $S(x)=\sum_{n\ge 1} u_n(x)$ est de classe $\mathcal C^1$ et $S'(x)=\sum_{n\ge 1} u'_n(x)$.

Caractère $\mathcal C^{\infty}$: Soit $I$ un intervalle, $(f_n)$ une suite de fonctions $\mathcal C^{\infty}$ de $I$ dans $\mathbb{R}$. On suppose que pour tout entier $k≥0$, la suite $(f_n^{(k)})$ converge uniformément vers une fonction $g_k:I→\mathbb{R}$ sur $I$.
Alors la fonction $g_0$ est de classe $\mathcal C^{\infty}$ sur $I$ et $g_0^{(k)}=g_k$.

Permutation limite/intégrale: Soit $I=[a,b]$ un segment et $(f_n)$ une suite de fonctions continues de $I$ dans $\mathbb{R}$ qui converge uniformément vers $f$ sur $I$. Alors:
$\displaystyle \lim_{n \to +\infty} \int_a^bf_n(t) dt=\int_a^b \lim_{n \to +\infty} f_n(t) dt$$=\int_a^b f(t)dt$

Permutation somme/intégrale: Soit $I=[a,b]$ un segment et $(u_n)$ une suite de fonctions continues. On suppose que $\sum_n u_n$ converge uniformément. Alors la série $\sum_n \int_a^b u_n(t)dt$ converge et:
$\int_a^b \sum_n u_n(t)dt= \sum_n \int_a^b u_n(t)dt$

4.4) Théorème des valeurs intermédiaires

4.5) Théorème de Rolle

Théorème: Soit $a < b$ deux réels et $f : [a, b] \rightarrow \mathbb{R}$ une fonction.
On suppose que:
- $f$ est continue sur $[a, b]$
- $f$ est dérivable sur $]a, b[$
- $f(a)=f(b)$

Alors, il existe (au moins) un réel $c \in ]a, b[$ dans tel que $f'(c)=0$

2 Lemmes que nous allons utiliser:
Lemme 1:
Soit $f : [a, b] \rightarrow \mathbb{R}$ continue. Alors $f$ est bornée et atteint ses bornes. En particulier, il existe $c_0$, $c_1 \in [a, b]$ tels que:
$f(c_0)=sup\{f(t); t \in [a, b]\}$
$f(c_1)=inf\{f(t); t \in [a, b]\}$
Lemme 2:
Soit $f : [a, b] \rightarrow \mathbb{R}$ dérivable sur $]a, b[$ et soit $c \in ]a, b[$. Si $f$ admet un extrémum local en $c$, alors on a $f'(c)=0$.

Raisonnement par disjonction des cas.
Premier cas: $f$ est constante. Alors, pour tout $c \in ]a, b[$, on a $f'(c)=0$.
Deuxième cas: $f$ n'est pas constante. Il existe donc $d \in ]a, b[$ tel que $f(d) \ne f(a)=f(b)$, par exemple $f(d) > f(a)=f(b)$.
Soit $c \in [a, b]$ tel que $f(c)=sup\{f(t); t \in [a, b]\}$. Alors $f$ admet un maximum global, donc local en $c$.
De plus $f(c) \geq f(d) > f(a)=f(b)$ et donc $c \in ]a, b[$. Par le Lemme 2, $f'(c)=0$.

4.6) Égalité et inégalité des accroissements finis

4.7) Fonction uniformément continue

4.8) Fonction lipschitzienne et contractante

Définition: Soient $E$ une partie de $\mathbb{R}$, $f : E \rightarrow \mathbb{R} $ une application et $k$ un réel positif. On dit que $f$ est $k$-lipschitzienne si $\forall (x,y) \in E^2, |f(x)-f(y)| \leq k|x-y| $
Définition: La fonction $f$ est dite contractante si on peut choisir $k < 1$.

Interprétation:

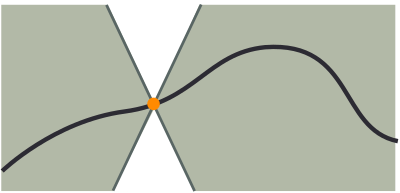
Une fonction réelle est $k$-lipschitzienne si le double cône blanc peut se déplacer le long de son graphe sans que jamais la courbe de la fonction passe à l'intérieur. Plus $k$ est petit, plus le cône blanc s'élargit et moins la fonction peut être abrupte.

Propriété 1: Une fonction lipschitzienne est uniformément continue.

Soit $f$ une fonction $k$-lipschitzienne sur $I$, et soit $\epsilon > 0$, alors si on pose $\eta = \dfrac{\epsilon}{k}$ on a:
$\forall \epsilon > 0, \exists \eta > 0, \forall (x,y) \in I^2,$ $(|x-y| \leq \eta \Rightarrow |f(x)-f(y)| \leq k \dfrac{\epsilon}{k}=\epsilon)$.

Exemples:
La fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\dfrac{1}{1+|x|}$ est uniformément continue.
En effet $|f(x)-f(y)|=\dfrac{||y|-|x||}{(1+|x|)(1+|y|)}$, or $||y|-|x|| \leq |x-y|$, donc:
$|f(x)-f(y)|\leq |x-y|$ ce qui signifie que $f$ est 1-lipschitzienne, et donc uniformément continue.

La fonction $f$ définie sur $\mathbb{R}_+$ par $f(x)=\sqrt{x}$ est uniformément continue.
En effet $|f(x)-f(y)|=|\sqrt{x}-\sqrt{y}| \leq \sqrt{|x-y|}$. En posant $\eta = \epsilon^2$ on montre que $f$ est uniformément continue.
Par contre $f(x)=\sqrt{x}$ n'est pas lipschitzienne, en effet $\dfrac{|f(x)-f(y)|}{|x-y|} \leq \dfrac{1}{|x-y|}$ avec $\dfrac{1}{|x-y|}$ qui tend vers $+\infty$ lorsque $x$ est proche de $y$.

La fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^2$ n'est uniformément continue et donc pas lipschitzienne (par contraposée).
...à venir

4.9) Fonction convexe et concave

Définition: Une fonction réelle d'une variable réelle est dite convexe si quels que soient deux points $A$ et $B$ du graphe de la fonction, le segment $[AB]$ est entièrement situé au-dessus du graphe, c'est-à-dire que la courbe représentative de la fonction se situe toujours en dessous de ses cordes.
$\Leftrightarrow$Une fonction $f$ est convexe sur $I$ lorsque, $\forall (x,y) \in I^2$, $\forall t \in [0;1]$ on a:
$f(tx+(1-t)y) \leq tf(x)+(1-t)f(y)$

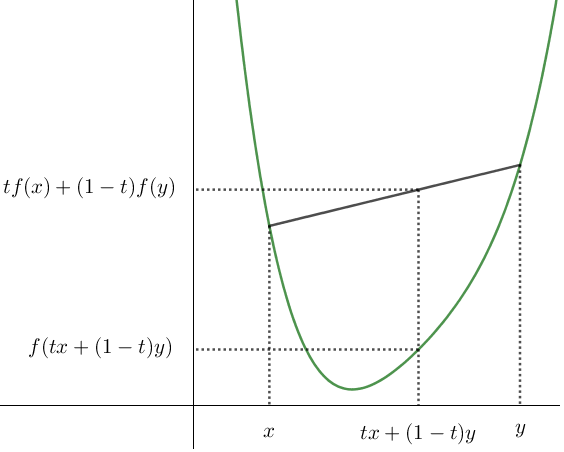
Une fonction est convexe ssi sa courbe représentative est au-dessous de ses cordes

En effet, faisons un petit calcul d'aire:
$\mathcal{A}_{grand-trapeze}=\mathcal{A}_{trapeze1}+\mathcal{A}_{trapeze2}$, d'où:
$\dfrac{(f(x)+f(y))(y-x)}{2}=$ $\dfrac{(f(x)+h)(1-t)(y-x))}{2}$ $+\dfrac{(h+f(y))t(y-x)}{2}$
$\Leftrightarrow f(x)+f(y)=f(x)-tf(x)+h+tf(y)$
$\Leftrightarrow h=tf(x)+(1-t)f(y)$

Une autre méthode est de calculer l'équation de la corde, puis de calculer l'ordonnée du point d'abscisse $tx+(1-t)y$

Définition: Une fonction $f$ est concave si $-f$ est convexe.
$\Leftrightarrow$Une fonction $f$ est concave sur $I$ lorsque, $\forall (x,y) \in I^2$, $\forall t \in [0;1]$ on a:
$f(tx+(1-t)y) \geq tf(x)+(1-t)f(y)$

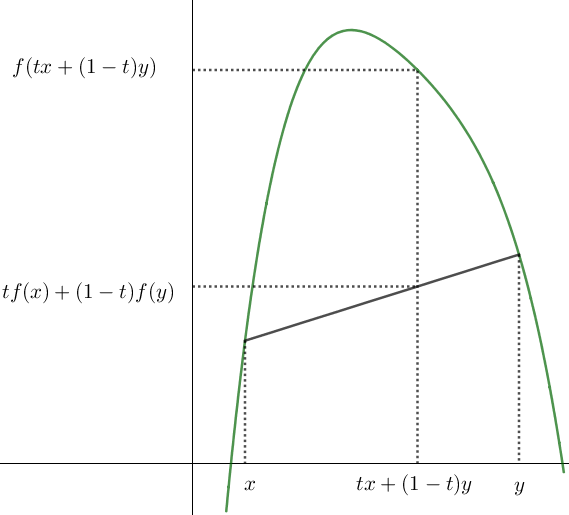
Une fonction est concave ssi sa courbe représentative est au-dessus de ses cordes

Théorème: Soit $f : I \rightarrow \mathbb{R}$. Les assertions suivantes sont équivalentes:
${\textstyle\unicode{x2460}}$ $f$ est convexe sur $I$
${\textstyle\unicode{x2461}}$ $\forall a \in I$, la fonction $x \mapsto \dfrac{f(x)-f(a)}{x-a}$ est croissante sur $I-\{a\}$
${\textstyle\unicode{x2462}}$ $\forall a,b,c \in I$ avec $a < b < c $, on a $\dfrac{f(b)-f(a)}{b-a} \leq \dfrac{f(c)-f(a)}{c-a} \leq \dfrac{f(c)-f(b)}{c-b}$

${\textstyle\unicode{x2460}}$ $\Rightarrow$ ${\textstyle\unicode{x2461}}$
Supposons $f$ convexe; posons $g(x)=\dfrac{f(x)-f(a)}{x-a}$ et soient $(x_1,a,x_2) \in I$.
Il faut donc montrer que si $x_1 \leq x_2$, alors $g(x_1) \leq g(x_2)$
Cas 1, $x_1 < a < x_2 $:
L'équation de la corde est $y(x)=\dfrac{f(x_1)-f(a)}{x_1-a}(x-a)+f(a)$
Or comme $f$ est convexe, $f(x_2) \geq y(x_2)$, càd $f(x_2)-f(a) \geq \dfrac{f(x_1)-f(a)}{x_1-a} (x_2-a)$
$\Leftrightarrow g(x_1) \leq g(x_2)$
Cas 2, $x_1 < x_2 < a $:
L'équation de la corde est toujours la même, mais par contre $f(x_2) \leq y(x_2)$, càd $f(x_2)-f(a) \leq \dfrac{f(x_1)-f(a)}{x_1-a} (x_2-a)$
$\Leftrightarrow g(x_1) \leq g(x_2)$

${\textstyle\unicode{x2461}}$ $\Rightarrow$ ${\textstyle\unicode{x2462}}$
Supposons que $\forall a \in I, \forall (x,y) \in (I-\{a\})^2$ avec $x < y$, $\dfrac{f(x)-f(a)}{x-a} \leq \dfrac{f(y)-f(a)}{y-a}$.
On veut prouver que $\forall (u,v,w) \in I^3$ tels que $u < v < w$:
$\dfrac{f(v)-f(u)}{v-u} \leq \dfrac{f(w)-f(u)}{w-u}$ $\leq \dfrac{f(w)-f(v)}{w-v}$
On pose $a=u$, $x=v$,$y=w$ et on obtient l'inégalité de gauche.
Ensuite on pose $a=w$, $x=u$,$y=v$ et on obtient l'inégalité de droite.

${\textstyle\unicode{x2462}}$ $\Rightarrow$ ${\textstyle\unicode{x2460}}$
Supposons que $\forall (a,b,c) \in I^3$, avec $a < b < c$ on a: $\dfrac{f(b)-f(a)}{b-a} \leq \dfrac{f(c)-f(a)}{c-a}$ $\leq \dfrac{f(c)-f(b)}{c-b}$
On veut prouver que f est convexe càd que $f(\lambda x+(1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y) $
On pose $a=x$, $b=\lambda x+(1-\lambda)y$ et $c=y$, on obtient:
$b-a=(1-\lambda)(y-x)$
$c-a=y-x$
$c-b=\lambda (y-x)$, d'où:
$\dfrac{f(\lambda x+(1-\lambda)y)-f(x)}{(1-\lambda)(y-x)}$ $\leq$ $\dfrac{f(y)-f(\lambda x+(1-\lambda)y)}{\lambda (y-x)}$
$\Leftrightarrow \lambda f(\lambda x+(1-\lambda)y) - \lambda f(x)$ $\leq$ $(1-\lambda)f(y)-(1-\lambda)f(\lambda x+(1-\lambda)y) $, d'où:
$f(\lambda x+(1-\lambda)y) \leq \lambda f(x) + (1-\lambda f(y))$

4.10) Fonction involutive

Définition: On dit que $f : E \rightarrow E$ est involutive si $\forall x \in E$, $f(f(x))=x$, autrement dit $f \circ f=id_E$.

4.11) Comparaisons asymptotique

Définition: Soit $a \in \mathbb{R} \cup \{+\infty; -\infty\}$. Soient $f$ et $g$ deux fonctions de la variable réelle $x$.
On suppose que $g$ ne s'annule pas sur un voisinage de $a$.
On dit que $f$ est négligeable devant $g$, et on note $f(x)=\underset{x \to a}{o}(g(x))$, lorsque $\displaystyle \lim_{x \to a} \frac{f(x)}{g(x)}=0.$
Exemples:
$x^2+10000=\displaystyle \underset{x \to \infty}{o} (x^3)$
$x^n=\displaystyle \underset{x \to +\infty}{o} (e^x)$

Définition: Soit $a \in \mathbb{R} \cup \{+\infty; -\infty\}$. Soient $f$ et $g$ deux fonctions de la variable réelle $x$.
On suppose que $g$ ne s'annule pas sur un voisinage de $a$.
On dit que $f$ est équivalente à $g$, et on note $ f(x) \underset{x \to a}{\sim}g(x)$, lorsque $\displaystyle \lim_{x \to a} \frac{f(x)}{g(x)}=1.$
Exemples:
$\cos(x)+x^{20}+e^x \underset{x \to \infty}{\sim} e^x$

Définition: Soient $f$ et $g$ deux fonctions de la variable réelle $x$.
On dit que $f$ est dominée par $g$ en $+\infty$, et on note $ f(x) = \underset{x \to \infty}{O}(g(x))$, lorsqu'il existe des constantes $N$ et $C$ telles que $\forall x > N, |f(x)| \leq C |g(x)|$.
De même si $a$ est un nombre réel, $f(x) = \underset{x \to a}{O}(g(x))$ s'il existe des constantes $d > 0$ et $C$ telles que $\forall x, |x-a| < d \implies |f(x)| \leq C |g(x)|$.
Exemples:
$x^3=\underset{x \to \infty}{O}(4x^3+10000x^2)$

4.12) Série de Fourier

Soit donc $f$ une fonction $T$-périodique, intégrable sur $[0,T]$ (par exemple, continue par morceaux). On appelle coefficients de Fourier trigonométriques de $f$ les nombres définis par :
$a_0(f)=\frac{1}{T} \int_0^T f(t)dt$
$\forall n \in \mathbb{N}^{*}$, $a_n(f)=\frac{2}{T} \int_0^T f(t) \cos(n \omega t)dt$
$\forall n \in \mathbb{N}^{*}$, $b_n(f)=\frac{2}{T} \int_0^T f(t) \sin(n \omega t)dt$

On appelle coefficients de Fourier trigonométriques de $f$ les nombres définis par :
$c_n(f)=\frac{1}{T} \int_T f(t)e^{-in\omega t}dt$
avec $\omega = \frac{2\pi}{T}$ (donc $\omega =1$ si $f$ est $2\pi$-périodique).
La fonction $f$ s'écrit alors:
$f(x)=\displaystyle \sum_{n=-\infty}^{+\infty} c_n(f)e^{in\omega x}$ ou encore $f(x)=a_0(f)$$+ \displaystyle \sum_{n=1}^{+\infty} a_n(f)\cos (n\omega x)$$+ b_n(f)\sin(n\omega x)$

$f(t)=\displaystyle \sum_{n=0}^{+\infty} a_n \cos(n \omega t) + b_n \sin(n \omega t)$, alors:
$\int_0^T f(t)dt=\int_0^T a_0 dt$ $+\displaystyle \sum_{n=1}^{+\infty} \int_0^T (a_n \cos(n \omega t) + b_n \sin(n \omega t))$
$\int_0^T f(t)dt=\int_0^T a_0 dt + 0$ (car $f$ est $T$-périodique et $\sin$ et $\cos$ sont $2\pi$-périodiques)
$\int_0^T f(t)dt=a_0T$

De même:
$\int_0^T f(t) \cos(p \omega t) dt$$= \displaystyle \sum_{n=0}^{+\infty} \int_0^T a_n \cos(n \omega t) \cos (p \omega t)dt$$+\displaystyle \sum_{n=0}^{+\infty} \int_0^T b_n \sin(n \omega t)\cos (p \omega t)dt $
$\int_0^T f(t) \cos(p \omega t) dt$$=a_n \frac{T}{2}+0$, d'où le résultat.
Avec la même méthode on trouve $b_n$.

4.13) Équations différentielles

Pour $n \in \mathbb{N}^{*}$, une équation différentielle linéaire d'ordre $n$ est une équation de la forme:
$a_n(x)y^{(n)}+a_{n-1}(x)y^{(n-1)}+...+a_0(x)y$$=b(x)$ où $a_0, a_1,...,a_n \in F(\mathbb{R},\mathbb{R})$ et $a_n \neq 0$.
Si $b(x)=0$, on dit que l'équation est homogène.

Posons $ \varphi (y)$$= a_n(x)y^{(n)}$$+a_{n-1}(x)y^{(n-1)}$$+...+a_0(x)y $.
Alors $ \varphi (y) $ est une application linéaire et l'ensemble des solutions sur $I$ de l'équation homogène est égal au noyau de $\varphi $.

Équations différentielles linéaires du 1er ordre.
Méthode:
- on cherche $y_0$ solution de l'équation homogène $(E_0)$
- on cherche $y_1$ une solution particulière de $(E)$
- on en déduit la solution générale de $(E)$ $y=y_0+y_1$
- on applique éventuellement une condition initiale à $y$

Pourquoi peut-on dire que $y=y_0+y_1$?

Supposons que $y$ soit solution de $(E)$, alors $a_1(x)y'+a_0(x)y=b(x)$.
Supposons que $y_1$ soit une solution particulière de $(E)$, alors $a_1(x)y_1'+a_0(x)y_1=b(x)$.
On a donc $a_1(x)(y-y_1)'+a_0(x)(y-y_1)=0$, autrement dit $y-y_1$ est solution de l'équation homogène $(E_0)$, donc $y-y_1=y_0$.

Pour déterminer $y_0$, on écrit l'équation différentielle homogène (E) sous la forme $ \frac{y'}{y}=a(x) $, ce qui donnera $ \ln |y| = A(x)+C $, soit $|y|=e^{A(x)+C}$, soit $y=\pm e^{A(x)+C}$.
On pose $K=\pm e^{C}$ et on obtient $y_0=K e^{A(x)}$ où $A(x)$ est une primitive de $a(x)$, et $K$ un réel.

Pour trouver une solution particulière on posera $y_1$ ressemblant au second membre. Si cette méthode ne fonctionne pas, on appliquera la méthode de variation de la constante.
Méthode de variation de la constante:
On pose $y_1(x)=K(x) e^{A(x)}$, puis on remplace dans $(E)$. On obtient une expression de $K'(x)$ et on en déduit $K(x)$.
On a donc trouvé une solution particulière $y_1(x)$.

Équations différentielles linéaires du 2nd ordre.

5) Probabilités

Formules générales de calcul de probabilités.
Formule de probabilité conditionnelle: $p(B|A)=p_A(B) = \frac{p(A\cap B)}{p(A)}$

$p(A \cup B) = p(A)+p(B)-p(A \cap B)$

Formule des probabilités totales: $p(A) = \displaystyle \sum_{i=1}^n p(E_{i})p(A|E_{i})$

Formules générales de l'espérance, et variance d'une variable aléatoire:
$ E(X)=\displaystyle \sum_{i=1}^{n} x_{i}P(X=x_{i})$
$ V(X)=E((X-E(X))^{2})$
$ V(X)=E(X^{2})-E(X)^{2}$
$E(X+Y)=E(X)+E(Y)$
$E(aX)=aE(X)$
$ V(X+Y)=V(X)+V(Y)$
$ V(aX)=a^{2}V(X)$
...à suivre

Loi de Probabilité	Espérance	Variance
de Bernoulli $P(X=1)=p$ $P(X=0)=1-p$	$p$	$p(1-p)$
Binomiale $P(X=k)=$ $\binom{n}{k} p^{k} (1-p)^{n-k}$	$np$	$np(1-p)$
Géométrique $P(X=k)=$ $(1-p)^{k-1}p$	$\frac{1}{p}$	$\frac{1-p}{p^{2}}$
Exponentielle	xxx	xxx
Normale	xxx	xxx
de Poisson	xxx	xxx

6) Algèbre

6.1) Groupe

Définition d'un groupe:
On appelle groupe tout couple $(G,*)$, où $G$ est un ensemble non vide auquel est associé une loi de composition interne qui vérifie les propriétés suivantes:
1) la loi * est associative: $\forall x,y,z \in G$, $x*(y*z)=(x*y)*z$
2) il existe un élément neutre $e \in G$: $\forall x \in G$, $x*e=e*x=x$
3) tout élément possède un symétrique: $\forall x \in G$, $\exists x^{-1} \in G$, $x*x^{-1}=x^{-1}*x=e$

Si de plus, la loi $*$ est commutative, on dit que le groupe est commutatif ou abélien.

Exemples:
$(\mathbb{Z},+)$ est un groupe, mais $(\mathbb{N},+)$ n'est pas un groupe.
Si $\mathbb{K}=\mathbb{Q}, \mathbb{R}$ ou $\mathbb{C}$, alors:
$(\mathbb{K},+)$, $(\mathbb{K}^n,+)$, $(M_{n,p},+)$ et $(\mathbb{K}[X],+)$ sont des groupes.
$(\mathbb{K}^{*},\times)$, $(GL_n(\mathbb{K}),\times)$ sont des groupes
$(\mathbb{Z}/n\mathbb{Z},+)$ et $((\mathbb{Z}/n\mathbb{Z})^{*},\times)$ et $(S_n,\circ)$ sont des groupes.

6.2) Anneau

Définition d'un anneau:
On appelle anneau tout triplet $(A, +, \times)$ formé d'un ensemble $A$ et de deux lois de compositions internes $+$ et $\times$ vérifiant:
1) $(A, +)$ est un groupe abélien de neutre noté 0 (ou $0_{A}$)
2) $\times$ est associative: pour tous $a,b,c \in A,$$ a \times (b \times c)=(a \times b) \times c$
3) $\times$ est distributive à gauche et à droite par rapport à la loi $+$, c'est-à-dire que pour tous $a,b,c \in A$, on a: $a \times (b+c)=a\times b + a \times c$ et $(b+c) \times a=b \times a + c \times a$

Si la loi$\times$ possède un élément neutre noté $1_A$, l'anneau est dit unitaire.
Si de plus, la loi $\times$ est commutative, on dit que l'anneau est commutatif.
Remarque: Dans un anneau $A$, tous les éléments $a \in A$ n'admettent pas forcément d'inverse pour la loi $\times$, mais si c'est le cas on dit que $a$ est inversible et on note son inverse $a^{-1}$.

Définition Morphisme d'un anneau:
Un morphisme d'anneaux est une application $f$ entre deux anneaux $A$ et $B$ qui vérifie les trois propriétés suivantes:
1) $f(a+b)=f(a)+f(b)$
2) $f(ab)=f(a)f(b)$
3) $f(1_A)=1_B$

Si de plus $f$ est bijective, on parle d'isomorphisme d'anneaux.

6.3) Algèbre

Définition d'une algèbre:
Soit $\mathbb{K}$ un corps. On appelle $\mathbb{K}$-algèbre un ensemble muni de deux lois internes $+$ et $\times$ et d'une loi externe sur le corps $\mathbb{K}$, notée $\cdot$, telles que:
1) $(E,+,\times)$ est un anneau
2) $(E,+,\cdot)$ est un espace vectoriel sur $\mathbb{K}$
3) Pour tout $\alpha \in \mathbb{K}$, pour tout $(x,y) \in E^2$ on a: $(\alpha \cdot x) \times y=x \times (\alpha \cdot y)=\alpha \cdot (x \times y)$

Si $E$ et $F$ sont deux algèbres, une application $f : E \rightarrow F $ est un morphisme d'algèbre si c'est un morphisme d'anneaux et une application linéaire.

6.4) Espace vectoriel et sous-espace vectoriel

Définition: Soit $E$ un ensemble muni d'une loi interne notée $+$ et d'une loi externe définie sur un couple $(\lambda, u)$ de $\mathbb{K} \times E$, et notée $\lambda u$. On dit que $E$ est un espace vectoriel sur $\mathbb{K}$, ou un $\mathbb{K}$-espace vectoriel, si:
1. $(E,+)$ est un groupe commutatif
2. Pour tous $(u,v)$ de $E$, pour tous $(\lambda,\mu)$ de $\mathbb{K}$, on a:
2.1. $\lambda (\mu,u)=(\lambda \mu)u$
2.2. $1u=u$
2.3. $(\lambda + \mu)u=\lambda u + \mu u$
2.4. $\lambda(u+v)=\lambda u + \lambda v$

Pour démontrer que $F$ est un sous-espace vectoriel de $E$, on applique la caractérisation des sous-espaces vectoriels, c'est-à-dire qu'on vérifie que:
- $0_{E} \in F$
- $\forall (x,y) \in F^2$ et tout scalaire $\lambda \in \mathbb{K}$, on a $ \left\{ \begin{array}{ll} x+y \in F\\ \lambda x \in F \end{array} \right. $

6.5) Formule de changement de base

Soit $E$ un espace vectoriel de dimension finie $n$ muni d'une base $\mathcal B_1=(e_1,...,e_n)$ et $\mathcal B_2=(\epsilon_1,...,\epsilon_n)$.
On appelle matrice de passage de $\mathcal B_1$ à $\mathcal B_2$ la matrice $P$ carrée de taille $n$, dont la $j$-ième colonne est formée des coordonnées de $\epsilon_j$ dans la base $\mathcal B_1$.

Soit $u$ un vecteur de $E$; notons $X$ ses coordonnées dans $\mathcal B_1$, et $X'$ ses coordonnées dans $\mathcal B_2$, alors $X=PX'$

On considère 2 bases $\mathcal B_1=(e_1,...,e_n)$ et $\mathcal B_2=(\epsilon_1,...,\epsilon_n)$ d'un même espace vectoriel $E$ de dimension $n$.
On considère un vecteur $u=a_{1}e_{1}+...+a_{n}e_{n}$ dans la base $\mathcal B_1=(e_1,...,e_n)$.
Supposons que ce vecteur $u$ s'écrive $u=b_{1}\epsilon_{1}+...+b_{n}\epsilon_{n}$ dans la base $\mathcal B_2=(\epsilon_1,...,\epsilon_n)$.
Si de plus on a:
$\epsilon_{1}=a_{11}e_{1}+a_{21}e_{2}+...+a_{n1}e_{n}$
$\epsilon_{2}=a_{12}e_{1}+a_{22}e_{2}+...+a_{n2}e_{n}$
...
$\epsilon_{n}=a_{1n}e_{1}+a_{2n}e_{2}+...+a_{nn}e_{n}$

Alors d'une part: $u= \begin{pmatrix} a_{1}\\ a_{2}\\ \vdots\\ a_{n} \end{pmatrix} $, et d'autre part: $u= \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n}\\ a_{21} & a_{22} & \dots & a_{2n}\\ \vdots & \vdots & \dots & \vdots\\ a_{n1} & a_{n2} & \dots & a_{nn} \end{pmatrix} \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{n} \end{pmatrix} $
$u=P \begin{pmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{n} \end{pmatrix} $ où $P$ est la matrice de passage de $\mathcal B_1$ à $\mathcal B_2$.
On a donc obtenu $X=PX'$ (ou encore $X^{'}=P^{-1}X$).

6.6) Changement de base pour un endomorphisme

Rappels:
On note $\mathcal L (E,F)$ l'ensemble des applications linéaires de $E$ dans $F$.
On note $\mathcal L (E)$ l'ensemble des endomorphismes.

*Application linéaire*: $\forall (x,y)\in E^{2},$$\;u(x+y)=$$u(x)+u(y)$ $\forall \lambda \in \mathbb {K},\;\forall x\in E,$$u(\lambda x)=\lambda u(x)$	*Isomorphisme*: Un isomorphisme est une application linéaire bijective. $\forall y\in F,\exists ! x\in E$$/f(x)=y$
*Endomorphisme*: Application linéaire de $E$ dans $E$	*Automorphisme*: Un automorphisme est un endomorphisme bijectif.

Soient:
-$f$ un endomorphisme de $E$
-$A$ une matrice carrée d'ordre $n$ associée à $f$ dans la base $\mathcal B$
-$A'$ une matrice carrée d'ordre $n$ associée à $f$ dans la base $\mathcal B'$
-$P$ la matrice de passage de $\mathcal B$ à $\mathcal B'$
-$X$ (resp. $X'$) et $Y$ (resp. $Y'$) les matrices colonnes des composantes des vecteurs $x$ et $y$ dans $\mathcal B$ (resp. $\mathcal B'$), alors si $y=f(x)$ on a:
$ \left\{ \begin{array}{ll} Y=AX & \text{juste un test}\\ Y'=A'X' \end{array} \right. $
De plus on a $X=PX'$ et $Y=PY'$.
D'où: $Y=PY'=PA'X'=PA'P^{-1}X$, soit $A=PA'P^{-1}$ (ou encore $A'=P^{-1}AP$).

6.7) Déterminant d'une matrice

Définition: Soit $A=(a_{i,j})_{1 \leq i,j \leq n}$. Le déterminant de $A$ noté $det(A)=\displaystyle \sum_{\sigma \in S_n} \varepsilon (\sigma) \prod_{j=1}^{n}a_{\sigma (j),j}$, où:
- $\sigma$ est la permutation
- $\varepsilon (\sigma)$ la signature de la permutation (vaut +1/-1)
- $S_n$ l'ensemble des permutations

6.7) Matrice inversible

Définition: Une matrice inversible est une matrice carrée $A$ pour laquelle il existe une matrice $B$ de même taille $n$ avec laquelle les produits $AB$ et $BA$ sont égaux à la matrice identité: $AB=BA=I_n$
Dans ce cas la matrice $B$ est unique, appelée matrice inverse de $A$ et notée $B=A^{-1}$.

Supposons qu'ils existent $B$ et $C$ deux matrices inverses de $A$, alors $B=BI_n=BAC=I_nC=C$

Théorème: Soit $M$ une matrice de $M_n(K)$. Elle est inversible ssi son déterminant est non nul.
De plus si $M$ est inversible, $det(M^{-1})=\dfrac{1}{det(M)}$

Quelques méthodes pour calculer l'inverse d'une matrice inversible $A$:
Méthode 1:
$Y=AX$, donc comme $A$ est inversible $X=A^{-1}Y$ il suffit donc simplement d'exprimer $X$ en fonction de $Y$.

Méthode 2:
Si un polynôme annulateur $P$ de $A$ dans $K[X]$ est connu, alors on peut facilement calculer son inverse.
Soit $P(X)=aX^{2}+bX+c$ un polynôme annulateur de $A$, alors on $P(A)=0$
$\Leftrightarrow aA^{2}+bA=-cI$
$\Leftrightarrow A(-\frac{1}{c})(aA+b)=I$
On a donc trouvé $B=-\dfrac{1}{c}(aA+b)$ telle que $AB=BA=I$.
Cette méthode peut aussi permettre de calculer les puissances de $A$.

6.8) Matrices semblables

Définition: deux matrices carrées $A$ et $B$ sont dites semblables (parfois noté $A \sim B$) s'il existe une matrice inversible $P$ telle que $A = P B P^{-1}$.

Propriété 1: Soit $(A,B) \in \mathcal M_n (\mathbb{C}) $, alors si $A$ est inversible $AB$ est semblable à $BA$.

$AB=ABAA^{-1}$

Propriété 2: Soient $A$ et $B$ deux matrices semblables, alors $A+I_n$ et $B+I_n$ sont semblables.

$P(B+I_n)P^{-1}=PBP^{-1}+I_n=A+I_n$

6.9) Diagonalisation

Préliminaires:
On ne peut diagonaliser que des matrices carrées.
Une matrice diagonale est une matrice dont les coefficients en dehors de la diagonale principale sont tous nuls; la matrice nulle est donc aussi une matrice diagonale.
Diagonaliser une matrice $M$, c'est chercher une matrice diagonale $D$ ainsi qu'une matrice inversible $P$ telle que: $M=PDP^{-1}$.
Autrement dit, on cherche une base dans laquelle la matrice M est diagonale.
La matrice $P$ est alors la matrice de changement de base (raison pour laquelle elle est inversible).

En fait, $M$ est la représentation matricielle d'un endomorphisme dans une base $E$, et $D$ la représentattion de ce même endomorphisme dans une base $F$.

Définition: Diagonaliser une matrice, c'est trouver une matrice de passage $P$ et une matrice diagonale $D$ telles que:
$A=PDP^{-1} \Leftrightarrow D=P^{-1}AP$.
Si $A=PDP^{-1}$, alors $AP=PD$.
Mais si $D$ est une matrice diagonale, multiplier $P$ par $D$ à droite revient à multiplier les vecteurs colonnes de $P$ par les coefficients diagonaux de $D$. Notons $v_i$ le $i$-ème vecteur colonne de $P$ et $\lambda_{i}$ le $i$-ème coefficient diagonal de $D$. Pour tout $i=1,...,n$, on doit avoir: $Av_i=\lambda_{i} v_i \Leftrightarrow (A-\lambda_iI_n)v_i=0$.
On dit que $v_i$ est un vecteur propre de $A$ associé à la valeur propre $\lambda_i$.

Parlons donc de ce qu'on appelle les éléments propres.
Les éléments propres sont les valeurs propres, les vecteurs propres et les sous-espaces propres associés aux valeurs propres.
Une valeur propre est un scalaire (souvent un réel): elle est souvent notée $\lambda$.
Un vecteur propre est un vecteur colonne, il est souvent noté $X$.
Un sous-espace propre est un espace vectoriel, il est souvent noté $E_{\lambda}$ s'il est associé à la valeur propre $\lambda$.
$X$ est un vecteur propre de $M$ si $X \neq 0$ et s'il existe un réel $\lambda$ tel que $MX=\lambda X$.
$\lambda$ est une valeur propre de $M$ s'il existe un vecteur non nul tel que $MX=\lambda X$.
Ainsi, une valeur propre possède une infinité de vecteurs propres, mais un vecteur propre ne peut associé qu'à une seule valeur propre.

Supposons maintenant qu'on ait une valeur propre $\lambda$ associée à un vecteur propre $X$, si on note $I_n$ la matrice identité:
$MX=\lambda X$, càd $MX-\lambda X=$, càd $(M-\lambda I_n)X=0$.
Ainsi $X \in \ker (M-\lambda I_n)$, donc $\ker (M-\lambda I_n) \neq \{0\}$, donc $M-\lambda I_n$ est non injective et $M-\lambda I_n$ est non inversible.

Parlons maitenant des sous-espaces propres.
Soit $\lambda$ une valeur propre, alors il y a au moins un vecteur propre associé, mais on a vu précédemment qu'il y a plusieurs vecteurs propres (tous ceux proportionnels à un vecteur propre).
Tous ces vecteurs propres sont rassemblés dans un espace vectoriel appelé sous-espace propre et noté $E_{\lambda}$.
On a donc par définition: $E_{\lambda}=\{X|MX=\lambda X\}$.
On notera que le vecteur nul fait partie de $E_{\lambda}$ sans pour autant être un vecteur propre. Le sous espace propre contient donc l'ensemble des vecteurs propres ainsi que le vecteur nul.

De la même manière qu'on regroupe l'ensemble des vecteurs propres d'une même valeur propre, on regroupe l'ensemble des valeurs propres d'une même matrice.
L'ensemble des valeurs propres d'une matrice est appelé le spectre de la matrice (noté Sp(M)).

Théorème: Une matrice $M$ de dimension $n$ est diagonalisable ssi la somme des dimensions des sous-espaces propres est $n$.
La concaténation des bases des sous-espaces propres forme alors une base de vecteurs propres de l'espace (qui pourra servir à former la matrice $P$).

Source_1

6.10) Trigonalisation

...à venir

6.11) Produit scalaire

Définition: Soit $E$ un espace vectoriel sur $\mathbb{R}$, et soit $f : E \times E \rightarrow \mathbb{R} $ une fonction. On dit que $f$ est un produit scalaire si:
- pour tous $u, v$ de $E$, $f(u,v)=f(v,u)$
- pour tous $u, v, w$ de $E$, $f(u+v,w)=f(u,w)+f(v,w)$
- pour tous $\lambda \in \mathbb{R}$, et tous $u, v$ de $E$, $f(\lambda u,v)=f(u,\lambda v)=\lambda f(u,v)$
- pour tout $u$ de $E$, $f(u,u) \geq 0$, avec égalité si et seulement si $u=0$

Autrement dit, un produit scalaire est une forme bilinéaire symétrique définie positive.

Définition: Un espace vectoriel sur $\mathbb{R}$ muni d'un produit scalaire est dit:
- euclidien s'il est de dimension finie
- préhilbertien s'il est de dimension infinie

Définition: Soit $E$ un espace vectoriel sur $\mathbb{C}$, et soit $f : E \times E \rightarrow \mathbb{R} $ une fonction. On dit que $f$ est un produit scalaire si:
- pour tous $u, v$ de $E$, $f(u,v)=\overline{f(v,u)}$
- pour tous $u, v, w$ de $E$, $f(u+v,w)=f(u,w)+f(v,w)$
- pour tous $\lambda \in \mathbb{C}$, et tous $u, v$ de $E$, $f(\lambda u,v)=f(u,\lambda v)=\lambda f(u,v)$
- pour tout $u$ de $E$, $f(u,u) \geq 0$, avec égalité si et seulement si $u=0$

Définition: Un espace vectoriel sur $\mathbb{C}$ muni d'un produit scalaire est dit:
- hermitien s'il est de dimension finie
- préhilbertien s'il est de dimension infinie

Exemples:
$ (f, g) \rightarrow \int_0^1 f(t)g(t)dt $ est un produit scalaire sur $ \mathcal C^0 ([0, 1], \mathbb{R}) $.
En effet, c'est bien une forme (application d'un $\mathbb{K}$-espace vectoriel dans $\mathbb{K}$, ici $\mathbb{K}=\mathbb{R}$ ), symétrique et bilinéaire et si $\int_0^1 f(t)^2dt=0$, alors $f(t)=0$ sur $[0, 1]$.
Par contre $ (f, g) \rightarrow \int_0^1 f(t)g(t)dt $ n'est pas un produit scalaire sur $ \mathcal C^0 ([-1, 1], \mathbb{R}) $, car l'intégrale peut être nulle et $f$ non nulle sur $[-1, 0]$.
De même, $ (f, g) \rightarrow \int_0^1 f(t)g(t)dt $ n'est pas un produit scalaire sur $ \mathcal C_{m}^0 ([0, 1], \mathbb{R}) $, car l'intégrale peut être nulle et $f$ non identiquement nulle.

6.12) Normes

Définition: Soit $E$ un espace vectoriel sur $\mathbb{K}=\mathbb{R}$ ou $\mathbb{C}$. Une norme sur $E$ est une application $N$ de $E$ dans $\mathbb{R_+}$, vérifiant les conditions suivantes pour tous $(x,y)$ dans $E$:
- $N(x)=0$ si et seulement si $x=0$
- $N(x+y) \leq N(x)+N(y)$ (inégalité triangulaire)
- $\forall \lambda \in \mathbb{K}, N(\lambda x)=|\lambda|N(x) $

L'espace $E$, muni de la norme $N$, s'appelle espace vectoriel normé.

La norme euclidienne
Soit $x=(x_1,…,x_n)$ un vecteur de $\mathbb{K}^n$.
La norme euclidienne est définie par:
$||x||=\displaystyle \sqrt{\sum_{k=1}^n x_k^2}=\displaystyle \sqrt{x_1^2+...+x_n^2}$

La norme p
On définit la norme $p$ par:
$||x||_p=\displaystyle (\sum_{k=1}^n x_k^p)^{\frac{1}{p}}$

La norme euclidienne est en fait la norme 2.

La norme infinie
On définit la norme infinie par:
$||x||_{\infty}=\displaystyle \max_{1 \leq i \leq n} |x_i|$

7) Résultats et valeurs à connaître

$S_{1}=\displaystyle \sum_{k=1}^n k=\frac{n(n+1)}{2}$

$S_{1}=\displaystyle \sum_{k=1}^n k=1+2+...+(n-1)+n$
$S_{1}=\displaystyle \sum_{k=1}^n k=n+(n-1)+...+2+1$
On a donc $2S_{1}=n(n+1)$, c'est-à-dire $S_{1}=\frac{n(n+1)}{2}$

$S_{2}=\displaystyle \sum_{k=1}^n k^{2}=\frac{n(n+1)(2n+1)}{6}$

On sait que $S_{1}=\displaystyle \sum_{k=1}^n k=\frac{n(n+1)}{2}$; posons $S_{2}=\displaystyle \sum_{k=1}^n k^{2}$.
On a $\displaystyle \sum_{k=1}^n k^{3}-(k-1)^{3}=n^{3}$ d'une part (somme télescopique).
D'autre part en utilisant la formule du binôme de Newton:
$(k-1)^{3}=k^3-3k^{2}+3k-1$
$\Leftrightarrow k^3-(k-1)^{3}=3k^{2}-3k+1$, d'où:
$\displaystyle \sum_{k=1}^n k^{3}-(k-1)^{3}=3S_{2}-3S_{1}+n=n^{3}$
D'où $S_{2}=\frac{n^{3}}{3}+\frac{n(n+1)}{2}-\frac{n}{3}=\frac{n}{6} (2n^{2}+3n+1)$
$S_{2}=\frac{n(n+1)(2n+1)}{6}$

$e \approx 2,71$
$\varphi = \frac{1+\sqrt{5}}{2} \approx 1,61$ est le nombre d'or (solution positive de l'équation $x^2=x+1$).
$\gamma \approx 0,58$ est la constante d'Euler. $\gamma = \displaystyle \lim_{n \to +\infty} ( \displaystyle \sum_{k=1}^n\frac{1}{k} -\ln(n))$
$\ln(2) \approx 0,69$; $\ln(3) \approx 1,10$
$\sqrt{2} \approx 1,41$; $\sqrt{3} \approx 1,73$

*Application linéaire*: \(\forall (x,y)\in E^{2},\)\(\;u(x+y)=\)\(u(x)+u(y)\) \(\forall \lambda \in \mathbb {K},\;\forall x\in E,\)\(u(\lambda x)=\lambda u(x)\)	*Isomorphisme*: Un isomorphisme est une application linéaire bijective. \(\forall y\in F,\exists ! x\in E\)\(/f(x)=y\)
*Endomorphisme*: Application linéaire de \(E\) dans \(E\)	*Automorphisme*: Un automorphisme est un endomorphisme bijectif.

Loi de Probabilité	Espérance	Variance
de Bernoulli \(P(X=1)=p\) \(P(X=0)=1-p\)	\(p\)	\(p(1-p)\)
Binomiale \(P(X=k)=\) \(\binom{n}{k} p^{k} (1-p)^{n-k}\)	\(np\)	\(np(1-p)\)
Géométrique \(P(X=k)=\) \((1-p)^{k-1}p\)	\(\frac{1}{p}\)	\(\frac{1-p}{p^{2}}\)
Exponentielle	xxx	xxx
Normale	xxx	xxx
de Poisson	xxx	xxx