
Objectif 1:
Déterminer la mensualité \( m \) qu'on aura à payer si l'on effectue un emprunt d'un capital \( C \) à un taux \( t \) qu'on décide de rembourser en \( n \) mois.Somme finale payée = Capital emprunté + intérêts, soit:
mensualité x nombre de mensualités = Capital emprunté + somme des intérêts de chaque mois, soit encore:
$$mn=C+\sum_{i=1}^{n}\frac{t}{12}C_{i} \hspace{1em}(1)$$ où:
\( \begin{cases} \text{$m$ = la mensualité} \\ \text{$n$ = le nombre de mensualité} \\ \text{$C$ = le capital emprunté} \\ \text{$t$ = le taux annuel} \\ \text{$C_i$ = le capital restant dû au ième mois} \end{cases} \)
Avec cette définition de \( C_i \), on peut écrire \( C_{1} = C \) et \( C_{i+1} = C_{i} - (m - \frac{t}{12}C_{i}) = C_{i}(1+\frac{t}{12}) - m \)
Or les mathématiques montrent (la démonstration par récurrence est évidente) que si une suite \( U_{n} \) peut s'écrire \( U_{n+1} = aU_{n} +b \) pour \( n \geq n_{0} \), alors: \( U_{n} = \frac{b}{1-a} + a^{n-n_{0}} (U_{n_{0}} - \frac{b}{1-a}) \)
En l'appliquant à notre cas, on obtient:
$$C_{i} = \frac{12m}{t} + (1+\frac{t}{12})^{i-1} (C - \frac{12m}{t}) \hspace{1em}(2)$$
Première méthode (la plus simple):
Après avoir payé le \( n \)-ième mois (dernier mois), le capital restant à rembourser est nul, c'est-à-dire \( C_{n+1}=0 \), ce qui revient à écrire: \( \frac{12m}{t} + (1+\frac{t}{12})^n (C - \frac{12m}{t}) = 0 \), d'où on obtient: $$\boxed{m = \frac{Ct/12}{1-(1+t/12)^{-n}}}$$
Deuxième méthode:
En partant de \( (2) \) on a: \( \frac{t}{12}C_{i} = m + (1+\frac{t}{12})^{i-1} (\frac{Ct}{12} - m) \), d'où:
\( \sum_{i=1}^{n} \frac{t}{12}C_{i} = nm + (\frac{Ct}{12} - m) \sum_{i=0}^{n-1} (1+\frac{t}{12})^i \) \( =nm + (\frac{Ct}{12} - m)(\frac{1-(1+t/12)^n}{-t/12})\) ...car \( \sum_{i=0}^{n-1}q^i=\frac{1-q^n}{1-q} \)
\( 0=C+ (\frac{Ct}{12} - m)(\frac{1-(1+t/12)^n}{-t/12}) \) ...car \( (1) \)
\( \frac{Ct}{12} - m = (\frac{Ct/12}{1-(1+t/12)^n}) \), soit \( m = \frac{Ct}{12}(1- \frac{1}{1-(1+t/12)^n})=-\frac{Ct}{12}(\frac{(1+t/12)^n}{1-(1+t/12)^n}) \) qui donne le résultat encadré.
Simulation:
Capital emprunté (en €) : (exemple 300000)
Taux annuel (en %) : (exemple 1,5)
Durée du prêt (en mois) : (exemple 240)
Objectif 2:
Déterminer la part des intérêts par rapport au capital emprunté.Les intérêts valent donc \( nm - C \)
\( nm - C = \frac{nCt/12}{1-(1+t/12)^{-n}} - C \)
\( nm - C = C(\frac{nt/12}{1-(1+t/12)^{-n}}-1) \)
Le rapport intérêts/(capital emprunté) vaut donc: $$\boxed{\frac{nm -C}{C}= \frac{nt/12}{1-(1+t/12)^{-n}}-1}$$
...à étudier avec un tableau de variations et/ou des graphiques, voir la suite.
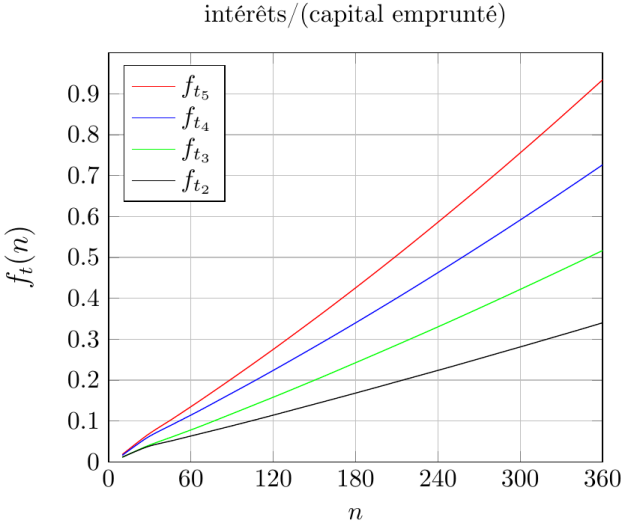
Posons \( f_{t}(n)=\frac{nm -C}{C}=\frac{nt/12}{1-(1+t/12)^{-n}}-1 \), et posons aussi \( t_{2}=2\%=0.02 \), \( t_{3}=3\%=0.03 \), \( t_{4}=4\%=0.04 \), \( t_{5}=5\%=0.05 \)
Voici un aperçu des variations de ce rapport pour ces 4 taux:
Objectif 3:
Déterminer la valeur des intérêts en fonction du mois, du taux et du capital emprunté.À partir de \( (2) \) en remplaçant \( m \) on obtient:
\( C_i=\frac{C}{1-(1+t/12)^{-n}} + \) \( (1+t/12)^{i-1}C(1-\frac{1}{1-(1+t/12)^{-n}}) \) d'où on obtient:
$$\boxed{C_i=C \frac{1-(1+t/12)^{i-n-1}}{1-(1+t/12)^{-n}}}$$
Ce résultat nous permet de calculer directement la valeur des intérêts pour un mois donné sans avoir à calculer les intérêts pour tout les mois précedents. Au passage, on vérifie bien que \( C_1=C \) et \( C_{n+1}=0 \). Notamment, il permettra (même si ce n'est pas indispensable) d'établir un tableau d'amortissement qui sera l'objectif 4.
