
1) Vie de Brahmagupta
Brahmagupta (598–670) est un mathématicien indien du VIIè siècle. Il vécut une grande partie de sa vie à Bhinmal, sous la protection des souverains de la dynastie des Gurjara. Il dirigea aussi l'observatoire de Ujjain, qui était le principal centre de recherche en mathématiques et en astronomie de l'Inde à cette époque. Il écrivit quatre traités, le plus important étant Brahmasphutasiddhanta, publié en 628 et écrit en vers, ce qui lui donne un intérêt poétique.
C'est dans l'oeuvre de Brahmagupta que, pour la première fois, le nombre zéro est réellement traité comme un nombre. Brahmagupta donne les règles des opérations utilisant ce nombre, même s'il se trompe en affirmant que 0/0 vaut 0. En revanche, il manie parfaitement les entiers négatifs, qui lui servent à représenter les pertes. Il sait résoudre les équations du second degré et de nombreuses équations diophantiennes.
Brahmagupta s'intéressa aussi à la géométrie. Il calcule l'aire d'un quadrilatère inscrit dans un cercle. Enfin, lors de ses travaux en astronomie, il estime la durée d'une année à 365 jours, 6 heures, 5 minutes et 19 secondes. C'est une très bonne approximation, puisque la vraie durée d'une année est d'un peu moins de 365 jours et 6 heures.
Il a fait ses travaux les plus remarquables à Ujjain, une ville qui était un centre important de l'astronomie et des mathématiques à cette époque.
2) Formule de Brahmagupta
On considère un quadrilatère de demi-périmètre \(p\) inscrit dans un cercle et dont les côtés mesurent \(a\), \(b\), \(c\) et \(d\):
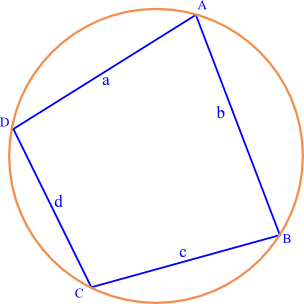
L'aire de ce quadrilatère est égale à : \(S=\sqrt{(p-a)(p-b)(p-c)(p-d)}\) où \(p\) est le demi-périmètre du quadrilatère c'est-à-dire \(p=\dfrac{a+b+c+d}{2}\).
Cette formule élégante est en fait une généralisation de la formule de Héron.
\(S=\dfrac{ab\sin \hat{A}}{2} + \dfrac{cd\sin \hat{C}}{2}\), or les angles opposés d'un quadrilatère cyclique sont supplémentaires autrement dit \(\hat{A}+\hat{C}=180°\) et \(\sin \hat{A}=\sin \hat{C}\), d'où:
\(S=\dfrac{ab\sin \hat{A}}{2} + \dfrac{cd\sin \hat{A}}{2}\)
\(S^{2}=\dfrac{\sin^{2} \hat{A}}{4}(ab+cd)²\)
\(4S^{2}=(1-\cos^{2} \hat{A})(ab+cd)²\)
\(4S^{2}=(ab+cd)²-\cos^{2} \hat{A} (ab+cd)²\) (*)
Par ailleurs, en appliquant 2 fois la formule d'Al-Kashi à BD, on a:
\(BD=a²+b²-2ab \cos \hat{A}=c²+d²-2cd \cos \hat{C}\) avec \(\cos \hat{C} = - \cos \hat{A}\), d'où:
\(2\cos \hat{A} (ab+cd)=a²+b²-c²-d²\)
En remplacant dans (*), on obtient:
\(4S^{2}=(ab+cd)²-\dfrac{(a²+b²-c²-d²)²}{4}\) et on reconnaît une identité remarquable, d'où:
\(16S^{2}=[2(ab+cd)+(a²+b²-c²-d²)][2(ab+cd)-(a²+b²-c²-d²)]\)
\(16S^{2}=[(a+b)²-(c-d)²][(c+d)²-(a-b)²]\) et on reconnaît une identité remarquable, d'où:
\(16S^{2}=[(a+b+c-d)(a+b-c+d)][(c+d+a-b)(c+d-a+b)]\)
Or \(p\) est le demi-périmètre du quadrilatère, donc:
\( \left\{ \begin{array}{llll} a+b+c-d=2(p-d)\\ a+b-c+d=2(p-c)\\ c+d+a-b=2(p-b)\\ c+d-a+b=2(p-a) \end{array} \right. \)
On obtient enfin: \(S=\sqrt{(p-a)(p-b)(p-c)(p-d)}\)
3) Théorème de Brahmagupta
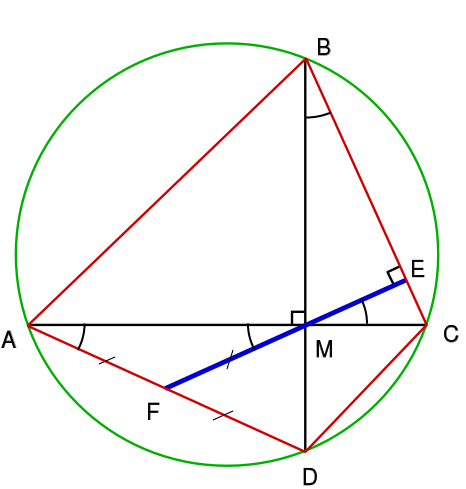
Théorème: Si un quadrilatère inscriptible a des diagonales perpendiculaires (autrement dit, est orthodiagonal) alors toute droite coupant perpendiculairement un côté quelconque du quadrilatère et passant par l'intersection des deux diagonales partage le côté opposé en deux parties égales.
On procède en démontrant que \(AF=FM\) et que \(FD=FM\).
\(\widehat{FAM}=\widehat{MBC}\) car on intercepte le même arc de cercle \(CD\).
Or \(\widehat{MBC}=\widehat{CME}\) car \(\widehat{EMB}\) et \(\widehat{CME}\) sont des angles complémentaires.
De plus \(\widehat{AMF}\) et \(\widehat{CME}\) sont opposés par le sommet, donc \(\widehat{CME}=\widehat{AMF}\).
Donc \(AFM\) est un triangle isocèle en \(F\) et \(AF=FM\).
De même, en utilisant les angles égaux \(\widehat{MDF}\) et \(\widehat{BCM}\), on obtient que le triangle \(DFM\) est isocèle en \(F\), donc \(FM=FD\).
Finalement \(AF=FD\).
